I recently delivered a 3.5 hour lecture on Extended Kalman Filters, discussing the subject from 0-100%, and I’d like to share some of that prep with you all.
First off, a disclaimer: this document will not teach you Kalman Filters. It is not intended to. Instead, it will teach you how to learn Kalman Filters. I will include here all of the resources and guidance that I think will be helpful for first ensuring that you have a solid grasp on the fundamentals you need, so that when you embark on learning Kalman Filters themselves, you’ll be well-armed. I will also include a recommended resources for learning Kalman Filters, as well as notes about the key chapters and concepts to pay attention to in that resource.
And with that, godspeed!
What’s the tl;dr?
Use this: Kalman and Bayesian Filters in Python, by Roger R. Labbe Jr
It’s a wonderfully unique text: hosted on github, written natively in Jupyter Notebook, and taking a Bayesian approach to understanding Kalman Filters, this text hits an amazing combination of simultaneously making the subject accessible and giving you the tools—even right within the text itself!—to tinker with it.
How do I use that?
Do you know programming?
If not, do this course from MIT on edX.
Do you know python?
If not, read this primer on python syntax from Learn X in Y Minutes.
As a side note, if you haven’t encountered it before, Learn X in Y Minutes is a fantastic resource for quickly coming up to speed on—or for reminding yourself about!—the syntax for just about every programming and programming-esque language under the sun.
Do you know how to install Jupyter Notebook?
If not, just get Anaconda, the premier scientific computing distribution for python.
Are you comfortable with linear algebra?
If not, I highly recommend doing this course from MIT OCW. Linear Algebra is the mathematical language behind Kalman Filters, and without fluency (quick test, can you explain what ABAᵀ means?), you will have difficulty.
As for that course itself, Gilbert Strang is somewhat of a legend, especially in the linear algebra community, and I cannot recommend highly enough pouring your time and energy into investing in a deep understanding of the fundamentals, like this linear algebra course. I have personally taken courses in linear algebra seven or eight times in my career, at least three of which have been repeated self-study of this very OCW course.
Plus, it’s convenient. There are about 24 lectures (read: episodes), and each is about an hour long (or only 30-40min, if you watch them on 1.5-2x speed, which I highly recommend; doing so makes the lectures much more exciting, and makes you much less likely to fall asleep during them! download and watch them with as fast of a playback speed as you can manage!). Now, 24 episodes is about one season of a TV show (or two, if they have shorter seasons like Stranger Things), and I know you’re capable of watching your way through one of those, so get to this! Watch the lectures. Do the problem sets. Learn linear algebra.
Are gaussians your friends?
If not, watch this video from Khan Academy. Non-negotiable. Gaussians and their properties are the sole reason why Kalman Filters work. You have to understand them if you want to succeed.
Do you understand Bayes’ Theorem?
If not, watch this video from 3Blue1Brown. The Bayesian perspective on Kalman Filters is the one adopted in the recommended text, and if you already understand Bayes’ Theorem going in, you’ll be well prepared.
Anything else I should know?
Do you know what a high-dimensional gaussian looks like?
If not, read this post. Even if you think you know what high-dimensional gaussians look like, read that post anyway. Seriously. Like, now.
There are many ways in which high-dimensional geometry departs from our expectations, and since most real-world Kalman Filters operate with at least a 4-5 dimensional state, you can quickly run into issues where your intuition will lead you astray. Build a better intuition! Unless you’ve got an advanced degree in mathematics, then you might have that intuition already, but you should still read that post because it’s a lot of fun.
Are Taylor Expansions your friends?
Ok, this one isn’t necessary for Kalman Filters themselves, but it is absolutely essential if you want to study the further topic of Extended Kalman Filters. It’s also a very common, and powerful, mathematical tool that shows up all over the place, so you should probably understand it.
Quick test: can you linearize a multi-dimensional function around an arbitrary point?
If not, start off with this video from 3Blue1Brown.
Follow it up with this video from Khan Academy.
And finish it off with this video from KristaKingMath.
What if I really don’t want to install anything?
Go here.
Then scroll down and click on this:
This will launch an interactive Jupyter Notebook session in your browser that’s backended by a remote server. It’s less ideal than just installing everything locally because you can’t save your work, and if you leave it alone for more than about 5 minutes, the remote server will shut down, and you’ll have to reload everything from scratch. But if you must, it’s there.
What if I’ve got Jupyter Notebook working, but I don’t know how to use git?
Go here.
Then click on this to download all of the files as a .zip archive.
Ok, so what’s the big deal about Kalman Filters?
If you’re not used to them, the math will look like alphabet soup.
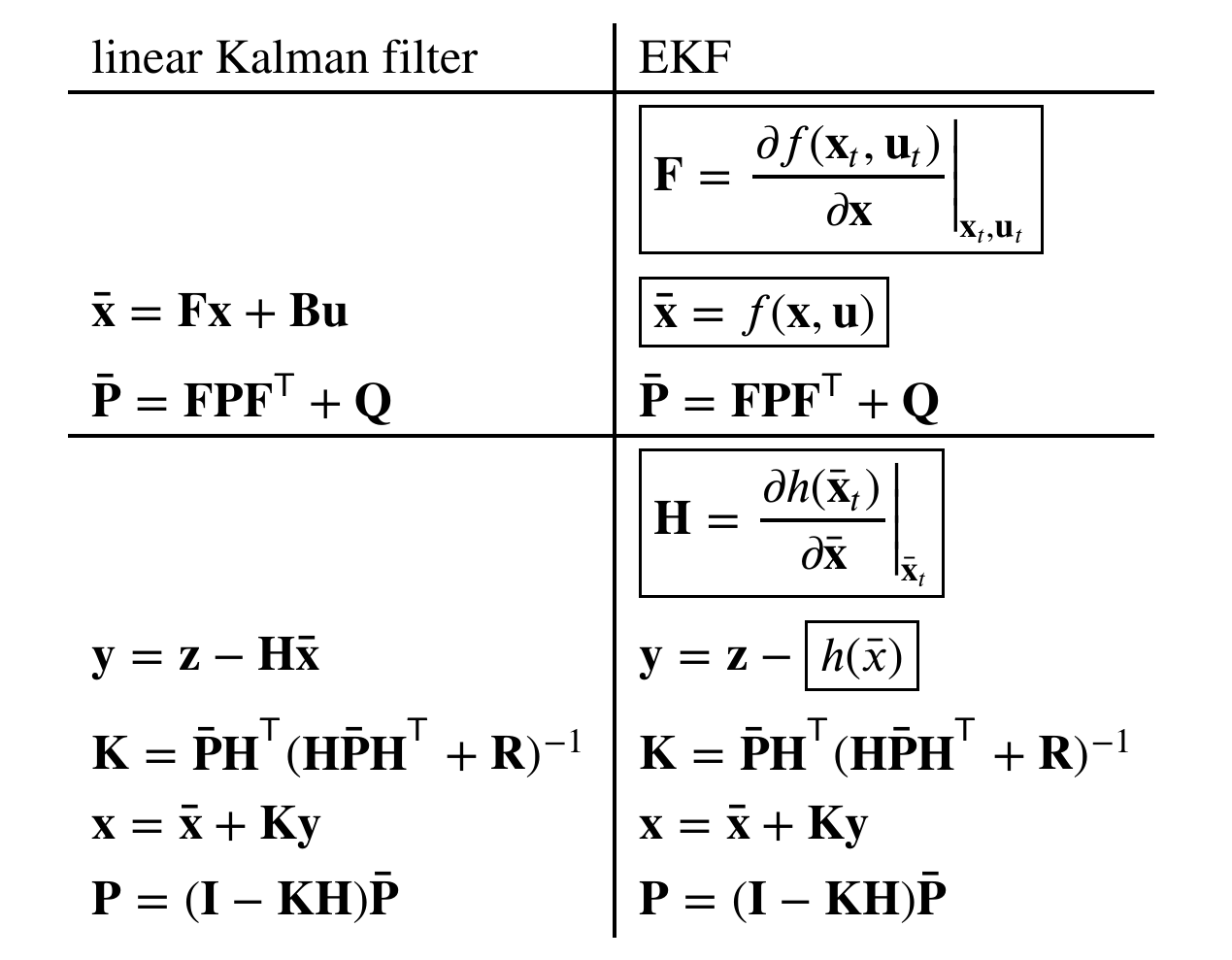screenshot from the text by R. Labbe linked above
No, I mean, what do they do? Why do I care?
Kalman Filters are a technique for taking noisy measurements from many sources and combining them in a mathematically optimal way.
They produce an estimate of some state, as well as uncertainties representing error associated with the estimate.
In this way, Kalman Filters are kind of like the opposite of deep learning.
Deep learning takes a ton of data, and tries to produce an OK result; but it doesn’t need a model of the system.
Kalman Filters take a minimum amount of data, and produce an optimal result; but you need to give them a model of the system.
Ok, but what do I really need to pay attention to in that text?
You mean this one?
-
Chapters 1-3 cover the basic ideas behind the whole field.
-
Chapter 4 introduces the basic Kalman Filter. Get comfortable with the notation here!
-
Chapter 7 gives you details on the math. If you get through this, you’re unstoppable.
-
Chapter 9 explains why we care about Extended Kalman Filters in particular.
-
Chapter 11 covers Extended Kalman Filters themselves.
-
Chapter 10 covers a more recent version, the Unscented Kalman Filter.